Algorithms for Finding all Possible Combinations of k Elements in an Array with Java Implementation

Given an array of size N e.g. e={'A','B','C','D','E'} N=5, we want to find all possible combinations of k elements in that array. For example, if k=3 then one possible combination is {'A','B','C'}. Here we have three different algorithms for finding k-combinations of an array.

Forward-Backward Algorithm

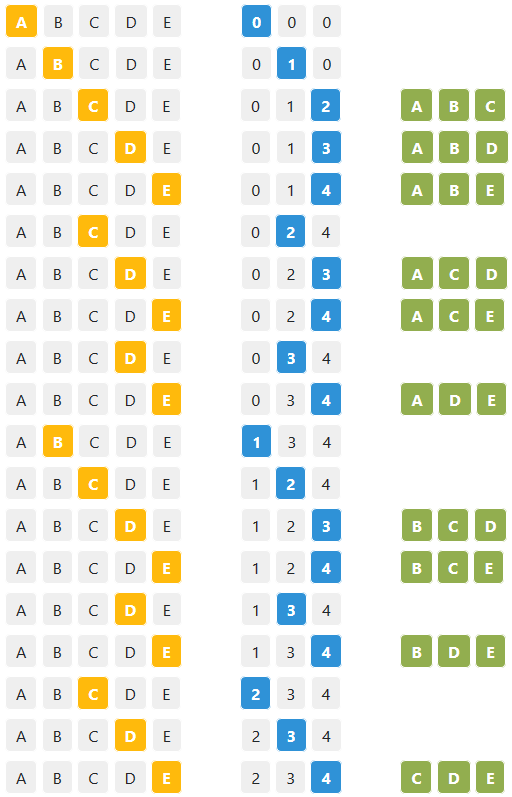
Here we have two arrays and two main indices r & i:

Array e which is the elements array.
Array pointers which is an array for holding indices for selected element.
Index i for pointing to current selected element in array e.
Index r for pointing to current position in pointers array.
The algorithm will move forward by incrementing i & r as long as they do not exceed arrays length.
If r reaches the last position of pointers array a combination is printed.
If both indices reach the last poisition of their pointing arrays the algorith will step backward by reducing r value r-- and set i with the value of i = pointer[r]+1.

combinations_forwardbackward

public static void combination(Object[]  elements, int k){

	// get the length of the array
	// e.g. for {'A','B','C','D'} => N = 4 
	int N = elements.length;
	
	if(k > N){
		System.out.println("Invalid input, K > N");
		return;
	}
		
	// init combination index array
	int pointers[] = new int[k];
	

	int r = 0; // index for combination array
	int i = 0; // index for elements array
	
	while(r >= 0){
	
		// forward step if i < (N + (r-K))
		if(i <= (N + (r - k))){
			pointers[r] = i;
				
			// if combination array is full print and increment i;
			if(r == k-1){
				print(pointers, elements);
				i++;				
			}
			else{
				// if combination is not full yet, select next element
				i = pointers[r]+1;
				r++;										
			}				
		}
		
		// backward step
		else{
			r--;
			if(r >= 0)
				i = pointers[r]+1;
			
		}			
	}
}

Shifting Algorithm

This algorithm is more intuitive than the first one.
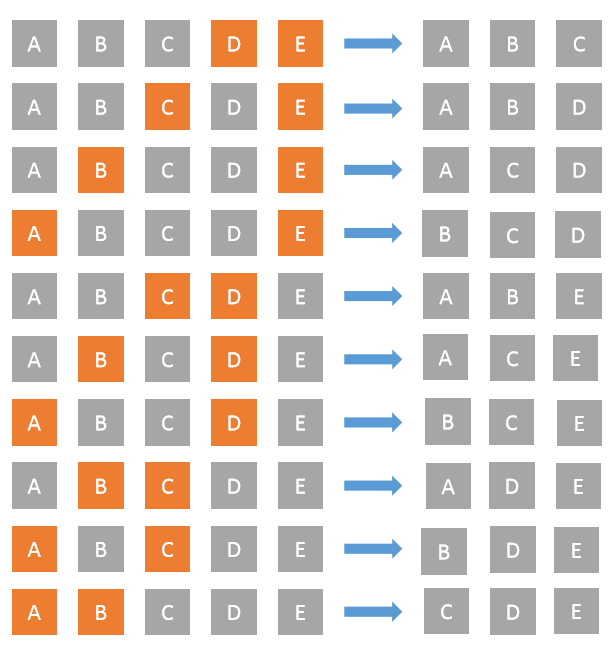
We virtually split the elements array into two types of elements, k elements that can be selected and N-k elements that will be ignored.
In each iteration we select N-k non-ignored elements.
After each iteration we shift the positions of ignored elements as shown in the image below.

combinations_shifting

public static void combination(Object[]  e, int k){

	int[] ignore = new int[e.length-k]; // --> [0][0]
	int[] combination = new int[k]; // --> [][][]
	
	// set initial ignored elements 
	//(last k elements will be ignored)
	for(int w = 0; w < ignore.length; w++)
		ignore[w] = e.length - k +(w+1);
	
	int i = 0, r = 0, g = 0;
	
	boolean terminate = false;
	while(!terminate){   
		
		// selecting N-k non-ignored elements
		while(i < e.length && r < k){
    			
    		if(i != ignore[g]){
    			combination[r] = i;
    			r++; i++;
    		}
    		else{	    			
    			if(g != ignore.length-1)
    				g++;	    			
    			i++;
    		}
    	}
    	print(combination, e);
    	i = 0; r = 0; g = 0;

    	terminate = true;
    	
    	// shifting ignored indices
    	for(int w = 0 ; w < ignore.length; w++){
    		if(ignore[w] > w){	    			
    			ignore[w]--;
    			
    			if(w > 0)
    				ignore[w-1] = ignore[w]-1;
    			terminate = false;
    			break;	    			
    		}
    	}
	}    		
}

Recursive Algorithm

Recursive algorithm has shorter steps.
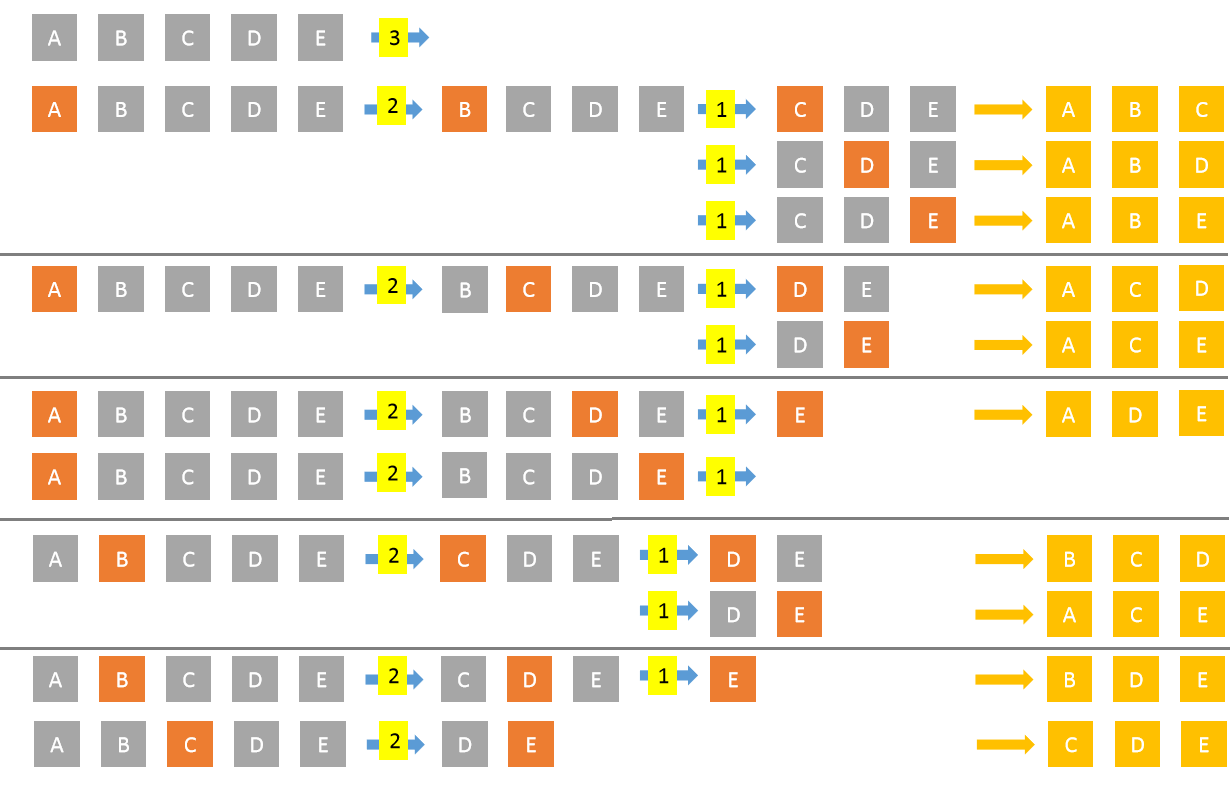
In each call to the function we pass List of elements, k and an accumulated combination.
Then we have four conditions:
1. if elements.length < k then stop
2. if k == 1 then add each element to the accumulated combination
3. if elements.length == k then add all elements to the accumulated combination.
4. if elements.length > k then for each element e make a recursive call passing sub list of the elements list, k-1 and add element e to accumulated combination.
It works as shown below

combinations_recursive

public static void combination(List<String> e, int k, String accumulated){

	// 1. stop
	if(e.size() < k)
		return;
	
	// 2. add each element in e to accumulated
	if(k == 1)
		for(String s:e)
			print(accumulated+s);
	
	// 3. add all elements in e to accumulated
	else if(e.size() == k){
		for(String s:e)
			accumulated+=s;
		print(accumulated);
	}
	
	// 4. for each element, call combination
	else if(e.size() > k)
		for(int i = 0 ; i < e.size() ; i++)
			combination(e.subList(i+1, e.size()), k-1, accumulated+e.get(i));
	
}

Forward-Backward Algorithm

Shifting Algorithm

Recursive Algorithm

Source Code @ GitHub